مبانی عددی از جمله مباحث مهم در رشته کامپیوتر و الکترونیک هست و از آنجا که به تازگی به موضوع AVR پرداختم لازم شد تا حتما یک مطلب در این باره بنویسم. مبنای عددی از گذشته های دور در ریاضیات وجود داشته و سبب شکل گیری دنیای دیجیتال شد. اعدادی که امروزه عموم مردم دنیا از آن ها استفاده می کنند مبنای ده هستند ولی افرادی هم بوده اند که از مبنا های عددی دیگر استفاده می کردند. امروزه مبنا های پرکاربرد دیگر شامل مبنای دو (باینری)، مبنای 8 (اوکتال) و مبنای 16 (هکس) هم هستند. به طور کل مبنای عددی روش ها گوناگون نمایش مقادیر عددی هست.
برای آن که بدانیم عدد در کدام مبنا هست آن ها را به این صورت می نویسیم: (1234)10 یا مثلا برای مبنای دو داریم (10110101)2
مبنای 10 (Decimal)
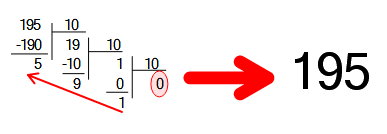
برای شروع مبحث مبنا پرداختن به اعدادی که در روزمره با آن ها سروکار داریم نقطه شروع خوبیه. در دوران ابتدایی در مورد جدول یکان، دهگان، صدگان و ... نقطه گفته بودند. درواقع اگر بخواهیم بجای اعداد 1، 10، 100، 1000 و ... (یا نوشتن یکان دهگان) از اعداد توان دار به شکل 100، 101، 102، 103، ... ، 10n استفاده کنیم جدولی مبنای عددی برای مبنای 10 داریم. پس عدد مبنا همیشه پایه ی این توان ها را مشخص می کند. از طرفی در هر مبنایی تنها مجازیم از ارقام کوچک تر از مبنا استفاده کنیم. این یعنی در مبنای ده تنها قادریم از ارقام 0 تا 9 استفاده کنیم، مثلا برای عدد 195 که یک عدد سه رقمی است تنها در ارقام 1، 9 و 5 استفاده شده (هیچگاه عدد 10 را به عنوان یک رقم در مبنای ده نداریم). برای جایگذاری عدد 195 در جدول مبنای عدد یک روش عمومی و یک روش سریع هست. البته چون به طور عمومی از مبنای 10 استفاده می کنیم پس نمایش مقدار و حاصل (عدد مبنا) به یک شکل خواهد بود. ولی این روش ها برای تبدیل مقادیر به مبنا های دیگر لازم است.
- روش اول: تقسیم متوالی: در این روش مقدار عددی را تقسیم بر مقدار مبنا می کنید، توجه کنید که تمام تقسیم ها صحیح هستند، باقی مانده را نگه داشته و مقسوم علیه را تقسیم بر 10 می کنیم و این کار را بار ها برای مقسوم علیه ها تکرار می کنیم تا زمانی که مقسوم علیه صفر شود. حال تمامی باقی مانده ها را به ترتیب از آخرین باقی مانده تا اولین از چپ به راست می نویسیم، عدد حاصل همان شکل مبنای مقدار عددی اول خواهد بود.
- روش دوم: تقسیم متوالی توان های مبنا: این روش کمی ساده تر و سریع تر هست، درواقع این روش مشابه همون روش جایگذاری عدد در جدول یکان دهگان هست. تو این روش اول بزرگ ترین مرتبه مناسب برای تقسیم مقدار عددی را پیدا می کنیم. مثلا در اینجا 100 هست. توجه کنید در این روش مقسوم علیه ها همگی باید تک رقمی باشند. و باقی مانده را تقسیم بر یک مرتبه پایین تر می کنیم (مثلا 10) تا جایی که باقی مانده دیگر بخش پذیر نباشد. حال نمایش مبنای عدد برابر است با کنار هم گذاشتن مقسوم علیه ها از اولین اون ها و آخرین باقی مانده.
مبنای دو (Binary)
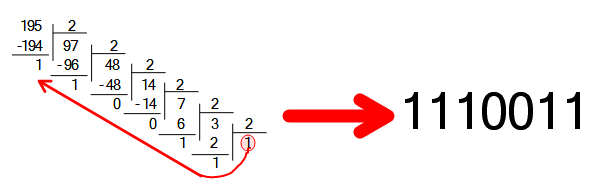
همانطور که پیش تر گفته بودم در مبنای دو قفط می توانیم از ارقام 0 و 1 استفاده کنیم. بدون در نظر گرفتن مبنا های کوچک تر از صفر (خیلی باحالن شاید بعد ها در موردشون بنویسم) کوچک ترین مبنا هست چون برای مبنای کوچک تر مثلا مبنای یک دیگر رقمی باقی نمی مونه! (فقط میشه از صفر استفاده کرد). نکته دیگه هم این که در اینجا مرتبه ها به شکل 20، 21، 22 و ... هست. به طور کل در اکثر مواقع هر چه مبنا کوچک تر باشد به تعداد ارقام بیشتر برای نمایش یک مقدار واحد نیاز است. پس بدونید که برای نمایش عدد 195 در مبنای 2 نیاز به تعداد ارقام بیشتر از 3 داریم.
در رایانه ها از مبنای دو استفاده می شود چون به سادگی می توان آن را به گونه های مختلفی مثل روشن و خاموش، آره و نه، درست و غلط و ... تفسیر کرد. به طور معمول در رایانه ها از 8 رقم یا بیت (Bit) استفاده میکنند که به آن یک بایت (Byte) می گویند. حداکثر مقدار یک بایت (مثبت) 255 است که در واقع تمام بیت ها 1 هستند
مسئله دیگر نمایش اعداد منفی است. روش های گوناگونی برای این کار هست.
برای نمایش اعداد منفی با ارزش ترین بیت (MSB-most significant bit یا به زبان ساده تر چپ ترین رقم) را به عنوان بیت علامت انتخاب می کنیم. کار این بیت این است که اعلام کند که عدد منفی می باشد. باقی ارقام بر اساس روش های مختلفی مثل علامت مقدار، متمم در مبنای کاهش یافته و متمم مبنا (چون برای تمام مبنا ها این روش ها قابل انجامند از کلمه مبنا استفاده شده؛ در اینجا می توانید عدد 2 را با کلمه مبنا جایگزین کنید که می شود متمم یک (کاهش یافته) و متمم دو) قابل انجام است. در تمامی این روش ها MSB بیت علامت است که در نتیجه اگر مثلا یک بایت (8-بیت) را در نظر بگیریم بسته به روش بازه اعداد مثبت تقریبا نصف می شود، چیزی در حدود 126
-
علامت-مقدار: همانطور که از اسمش پیداست یک عدد در این سیستم به سادگی شامل یک علامت و یک مقدار است مثلا عدد
(-12)10که خودش شامل یک علامت و مفدار است در مبنای دو (با هشت بیت) برابر می شود با(10001100)2. حال نکته مهم این است که در این شیوه دو صفر خواهیم داشت، صفر مثبت و صفر منفی؛ به این صورت:(00000000)2=+0و(10000000)2=-0البته که در دنیای واقعی صفر مثبت و منفی (مطلق یا غیر حدی) نداریم. با وجود سادگی این روش برای درک ما انسان ها استفاده از این روش در دنیایی کامپیوتر ها باعث پیچیدگی در محاسبات می شود. -
متمم در مبنای کاهش یافته (متمم یک): با فرض داشتن یک عدد n رقمی (مثلا برای یک بایت n=8) مانند N (برای مثال عددی مثال N=12) در مبنای r (در این جا r=2) ، متمم مبنای کاهش یافته (در اینجا متمم یک) به صورت
(rn-1)-Nتعریف می شود (یعنی برای نمایش عدد(-12)10در مبنای دو خواهیم داشت:(28-1)-12=(243)10=(11110011)2) البته توجه کنید که بیت سمت چپ (MSB) بیت علامت است که خود به خود در محاسبات یک میشه (که به معنی منفی بودن عدد هست). این در حالیت که نمایش مقدار مثبت عدد مورد نظر به این صورت است(+12)10=(00001100)2که این یعنی برای منفی کردن عدد 12 در مبنای r کافیست تمام ارقام از r-1 کم کنیم؛ مثلا در این جا که r=2 تمام ارقام را از r-1=1 کم می کنیم یا به زبان ساده تر یک ها را 0 و صفر ها را 1 کنیم. در این روش هم مانند روش قبلی دو صفر داریم:(00000000)2=+0و(11111111)2=-0. ولی در این روش محابات ساده تر است، برای مثال اگر بخواهیم عدد 12 را از 15 کم کنیم کافیست به سادگی عدد(-12)10=(11110011)2را با عدد(15)10=(00001111)2جمع کنیم. به مثال های زیر توجه کنید:
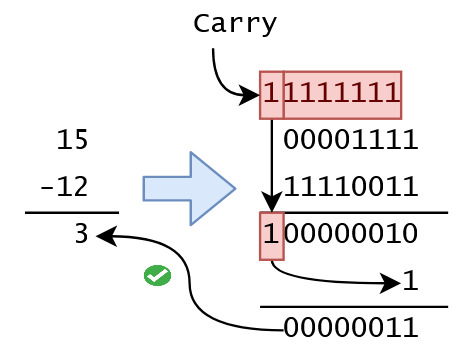

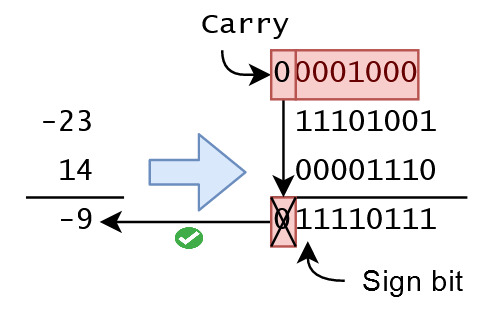
بیت حامل یا carry: اگر در مبنای ده باشیم برای جمع 5 با 38 یک عدد یک بالای 3 (دهگان 38) می گذاریم که در واقع دهگان حاصل جمع 8 با 5 هست است که می شوند 15، این کار برای آن است که حاصل جمع دو عدد کوچک تر از مبنا، برابر خود مبنا یا بیشتر شده. مثلا در جمع دو عدبرابر با دو د (1+1=2)10 = (01+01=10)2 حاصل جمع دو یک برابر با دو شده که برابر با مبنا است پس یک بیت کری با بیت بعدی جمع می کنیم.
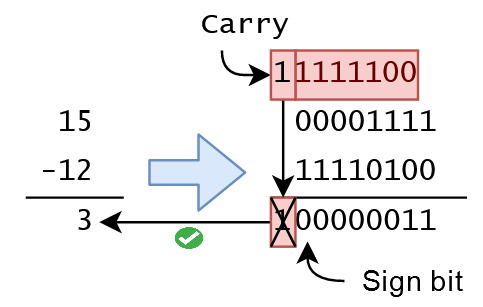
3. متمم مبنا (متمم دو): در دو روش قبلی دو صفر داشتیم و در روش دوم توانستیم محاسبه را راحت کنیم. این روش با هدف حذف صفر اضافی با حفظ سادگی محاسبه برای کامپیوتر است. با فرض داشتن یک عدد n رقمی (مثلا برای یک بایت n=8) مانند N (برای مثال عددی مثال N=12) در مبنای r (در این جا r=2) ، متمم مبنا (در اینجا متمم دو) به صورت rn-N تعریف می شود ( یعنی برای نمایش عدد (-12)10 در مبنای دو خواهیم داشت: 28-12=(244)10=(11110100)2) که یعنی برای منفی کردن 12 همانند روش قبل عمل می کنم و در آخر یک واحد با آن جمع می کنیم. به مثال های زیر توجه کنید:
بازه عددی در هر سه روش گفته شده:
| علامت مقدار | -127 | -0 | +0 | +127 |
| متمم یک | -127 | -0 | +0 | +127 |
| متمم دو | -128 | 0 | +127 | |
البته به طور پیشفرض تمام اعداد در هر مبنا را مثبت فرض می کنیم مگر آن که نویسنده عدد مستقیما به منفی بودن آن اشاره کند. در ادامه اعداد مثبت خواهند بود.
در اقلب زبان های برنامه نویسی برای تعیین نوع متغیر انواع بدون علامت متغیر ها با یک حرف U یا با کلمه unsigned مشخص می شوند مانند ubyte, uint, ulong و یا از حرف s یا کلمه signed برای متغیر های علامت دار استفاده می شود مانند sbyte.
امروزه در کامپیوتر ها برای کار با اعداد منفی روش متمم دو متداول است.
مبنای 3 (ternary)
مبنای سه در رایانه های ترنری استفاده می شود. اولین ماشین محاسبهای که با منطق سهسهای کار میکرد، یک ماشین محاسبه ساخته شده از چوب بود که در سال ۱۸۴۰ توسط توماس فاولر مخترع انگلیسی اختراع شد. نخستین رایانه مدرن الکترونیکی بر مبنای منطق سهسهای رایانهای به نام سِتون بود که اواخر دهه ۱۹۵۰ با راهبری پروفسور نیکلای بروسنتسوف در دانشگاه مسکو در اتحاد جماهیر شوروی ساخته شد. ستون مزایای قابل توجهی نسبت به رایانههای مبتنی بر منطق دودویی داشت، که از جمله آنها میتوان به مصرف برق و هزینه تولید کمتر اشاره کرد. در سال ۱۹۷۰، بروسنتسوف نمونه پیشرفتهتری از ستون را ساخت که ستون ۷۰ نام گرفت (بر گرفته از ویکی پدیا). البته منطق سه تایی به دو روش های مختلفی قابل پیاده سازی هست، در آینده مقاله ای در این باره می نویسم.
مبنای 8 (octal)
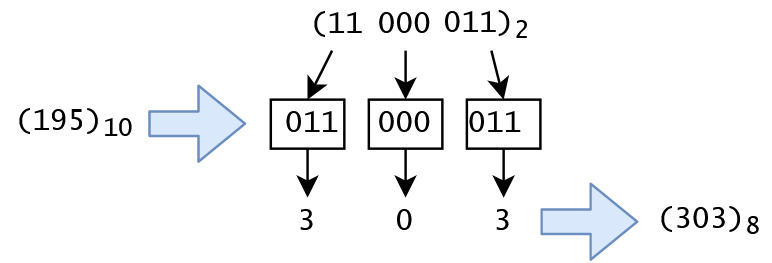
از دیگر مبنا های رایج مبنای هشت است. برای مثال اگر بخواهیم عدد 195 را در این مبنا بنویسیم می شود: 3*64+0*8+3*1=(303)8
در این مبنا خاصیت جالبی هم هست! از آنجا که این مبنا برابر است با 23=8 سبب شده تا هر سه بیت از یک عدد در مبنای دو برابر با یک رقم از این مبنا شود: (195)10=(11000011)2=(303)8
مبنای 16 (Hexage)
از پر کاربرد ترین مبنا ها مبنای 16 یا هکس است که جلو تر دلیل آن را خواهم گفت. برای مبنای 16 نیاز به 16 نویسه به عنوان ارقام داریم اما ما تنها از 0 تا 9 (10 رقم) داریم، پس به صورت قراردادی از حروف انگلیسی (معمولا حروف بزرگ) جای نویسه هایی با ارزش های 10 تا 15 استفاده می کنیم
| نویسه | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| مقدار | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
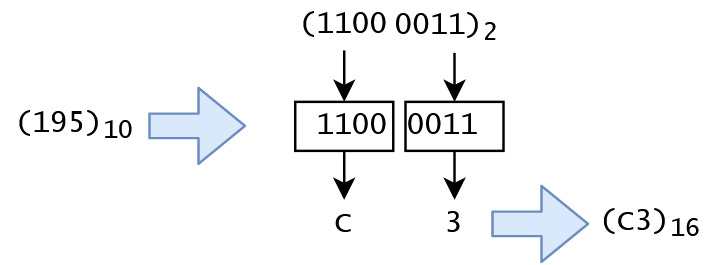
بنابر این اگر بخواهیم عدد 195 را در مبنای 16 نشان دهیم خواهیم داشت: 12*16+3*1=(C3)16
در این مبنا هم به این دلیل که 24=16 هر چهار بیت از عدد مبنای دو برابر با یک رقم از عدد مبنای 16 است: (195)10=(11000011)2=(C3)16
دلیل رواج بسیار این مبنا نمایش بیت ها به صورت خلاصه تر و در دو رقم است. (255)10=(11111111)2=(FF)16